MATRIKS
Matriks adalah susunan bilangan yang diatur menurut aturan baris dan kolom dalam suatu jajaran berbentuk persegi atau persegi panjang. Susunan bilangan itu diletakkan di dalam kurung biasa “( )” atau kurung siku “[ ]”.
Contoh:
Teguh, siswa kelas IX SMA Panca Budi, akan menyusun anggota keluarganya berdasarkan umur dalam bentuk matriks. Dia memiliki Ayah, dan Ibu, berturut-turut berumur 46 tahun dan 43 tahun.
Selain itu, dia juga memiliki kakak dan adik, secara berurut, Ningrum (22 tahun), Sekar (19 tahun), dan Wahyu (12 tahun). Dia sendiri berumur 14 tahun.
Berbekal dengan materi yang dia pelajari di sekolah dan kesungguhan dia dalam berlatih, dia mampu melakukan variasi susunan matriks yang merepresentasikan umur anggota keluarga Teguh sebagai berikut (berdasarkan urutan umur dalam keluarga Teguh).
Jenis matriks
A. Matriks Baris
Matriks baris adalah matriks yang terdiri atas satu baris saja. Biasanya, ordo matriks seperti ini adalah 1 × n, dengan n banyak kolom pada matriks tersebut.
b. Matriks Kolom
Matriks kolom adalah matriks yang terdiri atas satu kolom saja. Matriks kolom denagn ordo m × 1, dengan m banyak baris pada matriks tersebut.
C. Matriks Persegi Panjang
Matriks persegi panjang adalah matriks yang banyak barisnya tidak sama dengan banyak kolomnya. Matriks seperti ini memiliki ordo m × n.
d. Matriks Persegi
Matriks persegi adalah matriks yang mempunyai banyak baris dan kolom sama. Matriks ini memiliki ordo n × n.
e. Matriks Segitiga
Mari kita perhatikan matriks F dengan ordo 4 × 4. Terdapat pola susunan pada suatu matriks persegi.
F. Matriks Diagonal
Dengan memperhatikan konsep pada matriks segitiga di atas, jika kita cermati kombinasi pola tersebut pada suatu matriks pesegi.
g. Matriks Identitas
Mari kita cermati kembali matriks persegi dengan pola.
h. Matriks Nol
Jika entry suatu matriks semuanya bernilai nol, maka disebut matriks nol.
Kesamaan Dua Matriks
Matriks A dan matriks B dikatakan sama (A = B) jika dan hanya jika:
i. Ordo matriks A sama dengan ordo matriks B.
ii. Setiap entri yang seletak pada matriks A dan matriks B mempunyai nilai yang sama, aij = bij
(untuk semua nilai i dan j).
Tentukanlah nilai a, b, c, dan d yang memenuhi matriks Pt = Q, dengan
Karena P merupakan matriks dengan ordo 2 × 3, maka Pt merupakan matriks dengan ordo 2 × 3. Matriks Q merupakan matriks dengan ordo 2 × 3. Oleh karena itu berlaku kesamaan matriks Pt = Q.
Dari kesamaan di atas, kita temukan nilai a, b, c, dan d sebagai berikut.
• 3b = 3 maka b = 1, dan 2c = 6 maka c = 3.
• 2a – 4 = –4 maka a = 0.
• Karena a = 0 maka d = –3.
Jadi, a = 0, b = 1, c = 3, dan d = –3.
Operasi pada Matriks
Penjumlahan
Misalkan A dan B adalah matriks berordo m × n dengan entri-entri aij dan bij. Matriks C adalah jumlah matriks A dan matriks B, ditulis C = A + B, apabila matriks C juga dengan ordo m × n dengan entry-entry ditentukan oleh: cij = aij + bij (untuk semua i dan j).
Pengurangan
Matriks X dan Y memiliki ordo yang sama, yaitu berordo 3 × 2, sedangkan matriks Z dengan ordo 3 × 3. Oleh karena itu, menurut aturan pengurangan dua matriks hanya bagian i) saja yang dapat ditentukan, ii) dan iii) tidak dapat dioperasikan, (kenapa)?
Dari pemahaman contoh di atas, pengurangan dua matriks dapat juga dilakukan dengan mengurangkan langsung entry-entry yang seletak dari kedua matriks tersebut, seperti yang berlaku pada penjumlahan dua matriks, yaitu: A – B = [aij] – [bij].






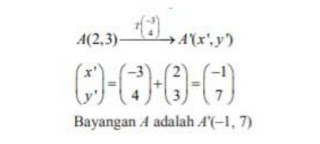
Comments
Post a Comment