Ema Janitra Kusuma

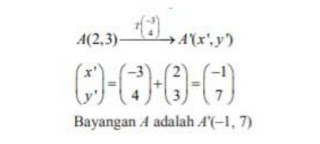
  Transformasi Menemukan Konsep Translasi ( Pergeseran ) Bangun yang digeser (translasi) tidak mengalami perubahan bentuk dan ukuran. Contoh Titik A(2, 3) ditranslasikan dengan matriks translasi T(–3, 4), tentukan bayangan A! Menemukan Konsep Refleksi (Pencerminan) Bangun yang dicerminkan (refleksi) dengan cermin datar tidak mengalami perubahan bentuk dan ukuran. Jarak bangun dengan cermin (cermin datar) adalah sama dengan jarak bayangan dengan cermin tersebut. Perhatikan gambar berikut! Coba kamu amati objek yang dicerminkan terhadap sumbu y pada bidang koordinat kartesius. Kamu terfokus pada jarak objek ke cermin dan jarak bayangan ke cermin serta bentuk/ukuran objek dan bayangan. Pencerminan Terhadap Titik O(0,0) Contoh Titik A(1, 4) dicerminkan terhadap titik asal O(0, 0), tentukan bayangan A! Pencerminan Terhadap Sumbu x Contoh Jika titik A(–3, 3) dicerminkan terhadap sumbu x maka tentukan bayangan titik tersebut! Pencerminan Terhadap Sumbu y Contoh Jika t

 Contoh: Siti dan teman-temannya makan di kantin sekolah. Mereka memesan 3 ayam penyet dan 2 gelas es jeruk di kantin sekolahnya. Tak lama kemudian, Beni dan teman-temannya datang memesan 5 porsi ayam penyet dan 3 gelas es jeruk. Siti menantang Amir menentukan harga satu porsi ayam penyet dan harga es jeruk per gelas. Jika Siti harus membayar Rp70.000,00 untuk semua pesanannya dan Beni harus membayar Rp115.000,00 untuk semua pesanannya. Jawab: Misalkan x = harga ayam penyet per porsi y = harga es jeruk per gelas Sifat-Sifat Determinan Sifat Misalkan matriks A dan B dengan ordo m × m dengan m ∈ N. Jika det A = |A| dan det B = |B|, maka |AB|= |A|.|B| Definisi Misalkan A sebuah matriks persegi dengan ordo n × n, n ∈ N • Matriks A disebut matriks nonsingular, apabila det A ≠ 0. • Matriks A disebut matriks singular apabila det A ≠ 0. • A–1 disebut invers matriks A jika dan hanya jika AA–1 = A–1A = I. I adalah matriks identitas perkalian matriks. diperoleh invers matriks A.

  Matriks adalah susunan bilangan yang diatur menurut aturan baris dan kolom dalam suatu jajaran berbentuk persegi atau persegi panjang. Susunan bilangan itu diletakkan di dalam kurung biasa “( )” atau kurung siku “[ ]”. Contoh: Teguh, siswa kelas IX SMA Panca Budi, akan menyusun anggota keluarganya berdasarkan umur dalam bentuk matriks. Dia memiliki Ayah, dan Ibu, berturut-turut berumur 46 tahun dan 43 tahun. Selain itu, dia juga memiliki kakak dan adik, secara berurut, Ningrum (22 tahun), Sekar (19 tahun), dan Wahyu (12 tahun). Dia sendiri berumur 14 tahun. Berbekal dengan materi yang dia pelajari di sekolah dan kesungguhan dia dalam berlatih, dia mampu melakukan variasi susunan matriks yang merepresentasikan umur anggota keluarga Teguh sebagai berikut (berdasarkan urutan umur dalam keluarga Teguh). Jenis matriks A. Matriks Baris Matriks baris adalah matriks yang terdiri atas satu baris saja. Biasanya,  ordo  matriks seperti ini adalah 1 × n, dengan n banyak kolom pada matr

  Program linear adalah metode yang digunakan untuk menentukan nilai optimum suatu persoalan linear. Nilai maksimum dan minimum atau nilai optimum bisa diperoleh dari nilai suatu himpunan penyelesaian persoalan linear. Dalam sebuah persoalan linear ada yang namanya fungsi linear yang biasa disebut dengan fungsi objektif. Lalu apa itu fungsi objektif? Nah, fungsi objektif adalah suatu fungsi linear yang berbentuk z = f (x,y) = ax + ay, digunakan untuk mencari nilai minimum atau maksimum setelah Anda menemukan titik pojok. Selain itu, program linear juga salah satu cara untuk menyelesaikan suatu soal yang berkaitan dengan nilai minimum dan maksimum dengan cara mengubah soal cerita menjadi sebuah model matematika.   Berikut ini adalah bentuk umum penulisan pertidaksamaan linear dua variabel: ax + by ≤ c; ax + by ≥ c; ax + by < c; ax + by > c; Keterangan: a, b, c adalah bilangan asli. a dan b adalah koefisien. c adalah konstanta. x dan y adalah variabel.

  INDUKSI MATEMATIKA induksi matematika adalah metode pembuktian yang sering digunakan untuk menentukan kebenaran.  Prinsip induksi matematika  adalah salah satu sifat penting dari bilangan bulat positif. Untuk memahami prinsip induksi matematika, simak pernyataan berikut ini. Misalkan  𝑃 ( 𝑛 ) adalah sifat yang didefinisikan untuk suatu bilangan asli  𝑛 , dan misalkan pula  𝑎  merupakan suatu bilangan asli tertentu. Dalam prinsip induksi matematika, apabila dua pernyataan berikut bernilai benar, maka: 𝑃 ( 𝑎 ) bernilai benar. Untuk sebarang bilangan asli  𝑘  ≥  𝑎 , apabila  𝑃 ( 𝑘 ) bernilai benar, maka  𝑃 ( 𝑘  + 1) juga bernilai benar. Oleh karena itu, pernyataan untuk sembarang bilangan asli  𝑛  ≥  𝑎 ,  𝑃 ( 𝑛 ) bernilai benar. METODE PEMBUKTIAN INDUKSI MATEMATIKA suatu pernyataan menyatakan “Untuk sembarang bilangan asli  𝑛  ≥  𝑎 , dengan  𝑎  adalah bilangan asli tertentu, sifat  𝑃 ( 𝑛 ) bernilai benar.” Agar dapat membuktikan pernyataan tersebut, diperlukan dua l